This is inspired by a very nice and entertaining Video on the Stand-Up-Math channel featuring Matt Parker and Hannah from NumberPhile.
They aimed to repeat an experiment from a book to measure the radius of the Earth with a very simple method, just measuring the angle between a horizontal line (perpendicular to the vertical) and a line to the visible horizon from a point with given height R. If the earth were flat, this angle would be zero. But otherwise, it depends on the radius of the Earth. With a bit of geometry, you see that the angle is equal to angle between the radial between you and the point were the tangent to the horizon touches the earth.
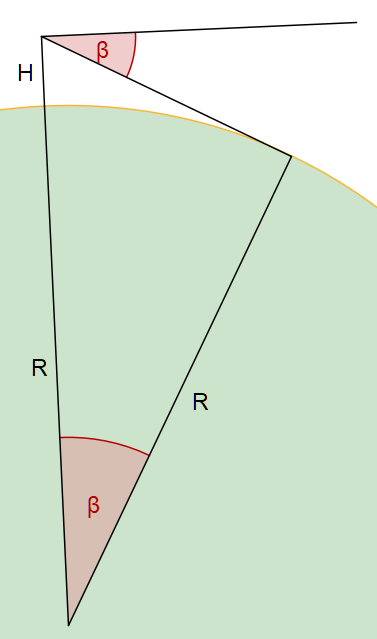
Thus
\cos(\beta) = \frac{R}{R+H} \Leftrightarrow R = \frac{\cos(\beta) H}{1-\cos(\beta)} \Leftrightarrow R = \frac{H}{1-\cosec(\beta)}If you wish, you can continue with this formula, or reformulate into a formula with the cosecans. For the practical purpose here, the angle is so small that we can replace it (using the development of the cosine) by
\beta^2 R = 2 H
In fact, the real numbers show that the angle for a 250m building or mountain is approximately half a degree.
The interesting twist of this video is that the measurement of the angle could only be taken with the inclinometer of a smartphone. It would have been far better to search for a horizontal structure and measuring the offset on as long a distance as possible when looking from one end to the horizon. In the end, their result turned off to be 1/10 of the real radius.
How do you estimate the error? The easiest and most practical way is to consider the relation of the relative errors of input and output. The idea for a function Y=Y(X) is the following
\frac{\Delta Y}{Y} = \frac{\Delta Y}{\Delta X} \frac{X}{Y} \frac{\Delta X}{X} \approx \left( Y'(X) \frac{X}{Y}\right) \frac{\Delta X}{X}The number in brackets is the magnification factor of the relative error. For an exponental, we get
Y= a X^n \Rightarrow Y'(X) \frac{X}{Y} = nIn our case the radius depends with n=-2 from the angle. The relative error simply doubles, R getting smaller if the angle gets larger. Thus you have to measure the small angle of half a degree with 5% accuracy to get a 10% accuracy in the radius. On a hazy day, when you cannot see the horizon properly, this is close to impossible. If you have a 1m stretch of something horizontal (perpendicular to the vertical), the offset will only be 8mm, the breadth of a thumb. On a 1000m high mountain, it is much easier because the angle is larger and you can build bigger and more fancy instruments to measure it.
Matt pointed out that the ancients might have some trouble to determine the height of a mountain relative to a calibrated distance on the ground. To overcome this problem, a simple triangulation can be used. We can measure the angle of the mountain top from the horizontal from a distance D, the step back a calibrated distance C, and measure the angle again. The trigonometric equalities read
H = \tan(\alpha_D) D = \tan(\alpha_{D+C}) (D+C)From C and the angles, D can be computed and thus H. The factor of the relative errors depend on the difference between the two measured angles.
That is, if you know to compute the tangent function. If not, the easiest way is to make a small sketch of the situation with correct angles and compute the proportions between the C and the H in that sketch.
One should finally mention that the radius of the earth has indeed be measured with 4% accuracy by Eratosthenes in 240 B.C. At least, this is the earliest known measurement. The method involved the length of the shadows in Alexandria, Egypt, and Syene, Greece. The main problem might be to learn the distance between these places relative to a calibrated distance in a stadium.