
This construction works without stretching or bending. Everything is sitting exactly on the studs. Here is a mathematical abstraction of the situation.
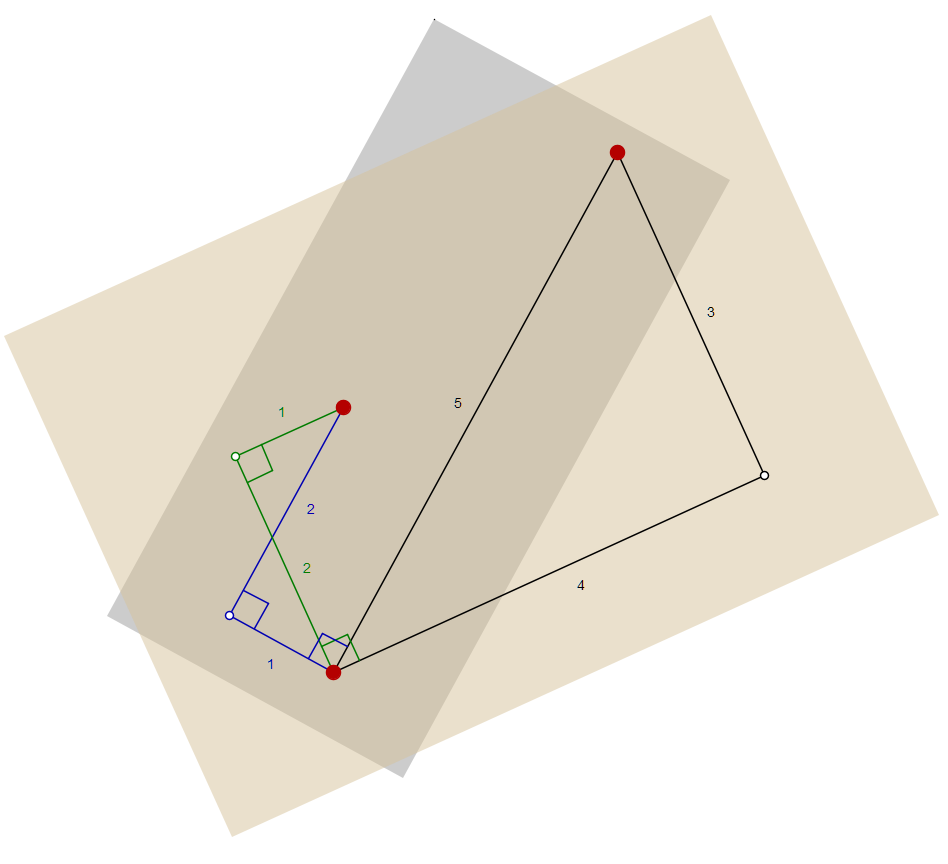
This has been observed by a friend who gladly noticed that it’s not self-evident and indeed interesting. His set of Duplo stones has little flowers which work as 1×1-stones extending single studs. That way you can fix a second board on the lower board. If the flowers are placed on the red spots, the upper board fits exactly to all three spots in the angle shown above. Why is that working?
The blue and green triangle can be constructed in a half circle by a fact named after Thales. You can make the blue one rectangular to the side of length 5. But why is the green one rectangular to the side of length 4?
Obviously we have to compute the angle between the blue side of length 1 and the green one of length 2. It must be the same as the angle in the Pythagorean 3-4-5 triangle. We need to prove
\arctan(2) - \arctan(\frac12) = \arctan(\frac34)
To do this, we can use known addition rules for the arctan function. Those can be derived using complex numbers. We use
\arctan(x) = \arg(1+ix)
Since angles add when complex numbers are added, we get
\arctan(x)+\arctan(y) = \arg((1+ix)(1+iy)) = \arg(1-xy +i(x+y)) \\ = \arctan(\frac{x+y}{1-xy})Using this, we see
\arctan(\frac12) + \arctan(\frac34) = \arctan(\frac{1/2+3/4}{1-3/8}) = \arctan(2)A former colleague of mine pointed out that it can be done without computations involving trigonometric functions. Assume, we do not know the sides of the green triangle. We know only that it is rectangular to the side of length 4. Then it is possible to compute the sides using the similarity of two triangles formed between the green and blue line segments, and the black one with side ratio 3/4.
Here is another way of looking at the situation.
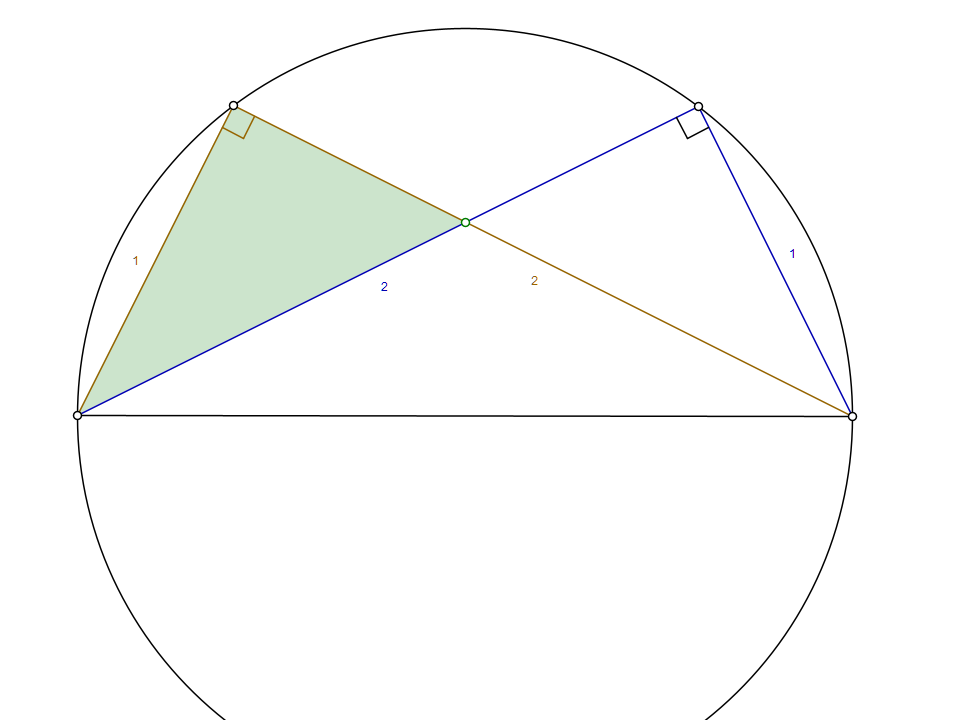
We just saw that the green triangle has a side ratio of 3/4 and is similar to the Pythagorean triangle 3-4-5. But can we see that from the sketch above?
If we divide the blue line by the intersection point into to segments of length a and b, we see
a+b = 2, \quad 1+a^2 = b^2
with the solution
a = \frac54, \quad b = \frac34
It always surprises me, how nice mathematics can be discovered even in everyday toys.