Recently, some YouTube videos came up in my inbox that refer to an article in the Scientific American. It seems, I cannot read this article without a subscription. But there is a rather complete sketch on a site called IFL Science, which I can link to and read. Hopefully, the link is permanent.
Anyway, the story is that two high school students prove the theorem of Pythagoras with methods „which were thought impossible till now“. In the last step, they used
\sin(2 \alpha) = 2 \sin(\alpha) \cos(\alpha).
The claim goes that this prove is based on this identity, and that this was not possible to date. I have to admit, that the computations these students used are quite astonishing and I admire their effort. I wish I had more like those students when I was active.
The truth is, however, that the proof uses similarity heavily. This is a problem because there are easy proofs for the theorem of Pythagoras using similarity only.
The proof of these students uses the same methods as other proofs, plus the additional use of a non-trivial trigonometric identity.
I would certainly reject this as a referee if it contained the claim that the methods are new. But it is a nice computation and as such to be acclaimed.
Of, course I need to explain to you what is going on. It is a bit involved, and I only have access to a secondhand version, but follow me through the reasoning as I understand it.
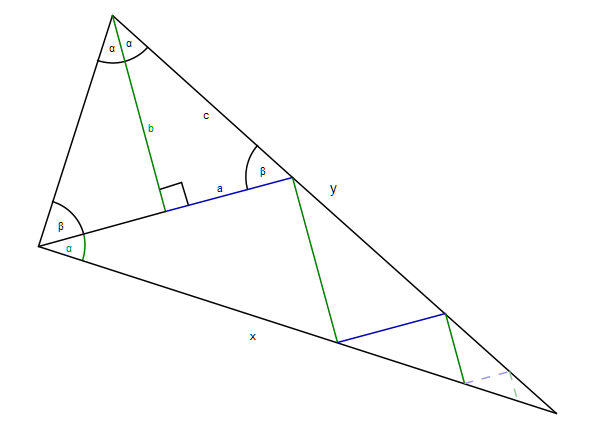
How the sketch above is done should be self-evident. You just need to know that the green lines and the blue lines are parallel. Thus, the red/blue zigzag line is formed by turning rectangular whenever it meets the black line.
Note, that the black triangle is rectangular. We get
\frac{x}{y} = \sin(2\alpha) = 2 \sin(\alpha)\cos(\alpha) = \frac{2ab}{c^2}.For my argument, it is crucial to notice that we already used the trigonometric identities for sine and cosine in a rectangular triangle, and also the non-trivial trigonometric identity cited above.
In the next step, they compute x and y as an infinite sum. If we look at x, we see that it consists of black segments which become smaller and smaller in a given proportion. The first segment of x has the length
x_1 = \frac{2a}{\cos(\alpha)} = \frac{2ac}{b}.The first segment of y is c.
y_1 = c.
The length of the next segment is more complicated. Using the second green line segment, we get
y_2 \cos(\alpha) = x_1 \sin(\alpha)
Thus
y_2 = \frac{2 a^2}{b^2} cWe can now compute the shrinking factor by comparing the second blue line with 2a.
\gamma = \frac{\sin(\alpha) y_2}{2a} = \frac{a^2}{b^2}. Thus, adding up the infinite sum for x,
x = x_1 (1+\gamma+\gamma^2+\ldots) = \frac{x_1}{1-\gamma} = \frac{2abc}{b^2-a^2}.And, similar for y,
y = c + \frac{y_2}{1-\gamma^2} = c + \frac{2a^2c}{b^2-a^2} = \frac{(a^2+b^2)c}{b^2-a^2}.Consequently,
\frac{x}{y} = \frac{2ab}{a^2+b^2}.If we compare to the formula for x/y above, we get the theorem of Pythagoras.
a^2+b^2 = c^2.
Clearly, this is a nice computation. But what have we actually used?
Indeed, we have used the identities
\sin(\alpha) = \frac{a}{c}, \quad \cos(\alpha) = \frac{b}{c}in rectangular triangles with sides a, b, c and angle alpha. But if this is valid, we have used the law of similarity, at least for rectangular triangles. This law says, that similar triangles, i.e., triangles with equal angles, have the same proportions between corresponding sides.
Now we have the problem, that there are very easy proofs for the theorem of Pythagoras using similarity only. The easiest one is from the sketch below.
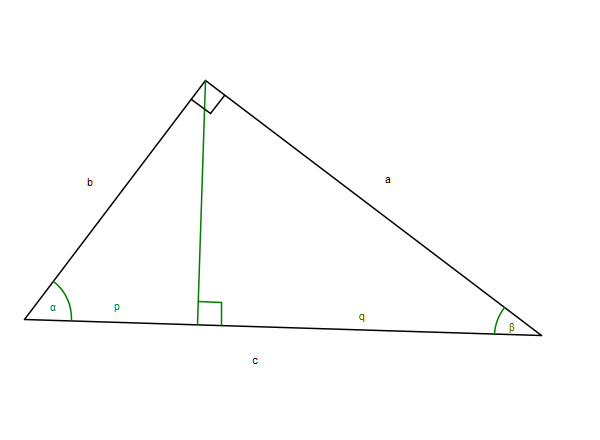
We have three similar triangles here: The big one with sides a, b, c, and the two parts of it. Using similarity, we get
\frac{b}{p} = \frac{c}{b}, \quad \frac{a}{q}=\frac{c}{a}.Thus, immediately,
a^2+b^2 = pc+qc = (p+q)c = c^2.
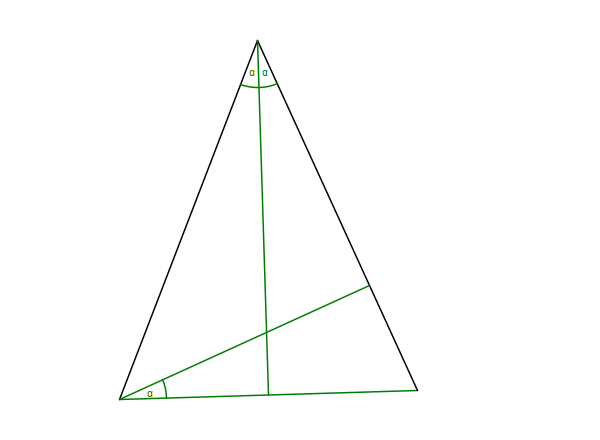
By the way, you will also need similarity to prove the trigonometric identity we started with. I leave the details for you to discover. But the basic sketch is the following.
The strange claim that it is impossible to prove the theorem of Pythagoras with trigonometry only is also false. The simplest way I came up with is to use the addition laws for sine and cosine and some facts about Pi. The essential line goes like this.
1 = \sin(\pi/2) = \sin(x+(\pi/2-x)) \\ = \sin(x)\cos(\pi/2-x)+\cos(x)\sin(\pi/2-x) \\ = \sin(x)^2+\cos(x)^2
To prove the last identity, you need to apply the addition law for cosine and sine again.